

The result is f( n) = -9 n + 78, which works for every value of n.

Fix this by simply adding 78 in the formula. However, notice that this formula is off by 78 for every number in the given sequence. Since each number is nine less than the last, the formula will be something like f( n)=-9 n. A much easier method is to find a formula f( n) for the nth number in the sequence and then plug in 31 for n. Thus, a straightforward way to calculate the 31st term is to write out the first 31 terms in the sequence, but this would be very tedious. The pattern is that every number is nine less than the previous number. Therefore, the next number will be 5 more than the last number.ġ0. Calculate the difference between consecutive numbers. Therefore, the next four numbers are 162, 243,. Multiply 108 by to find the next number in the sequence.Ĭontinue multiplying to find the next three numbers in the sequence. The pattern is that every number is times the previous number. Substitute 23 for n in this formula and calculate.Ĩ. The result is f( n) = 6 n + 3, which works for every value of n. Fix this by simply adding 3 in the formula.
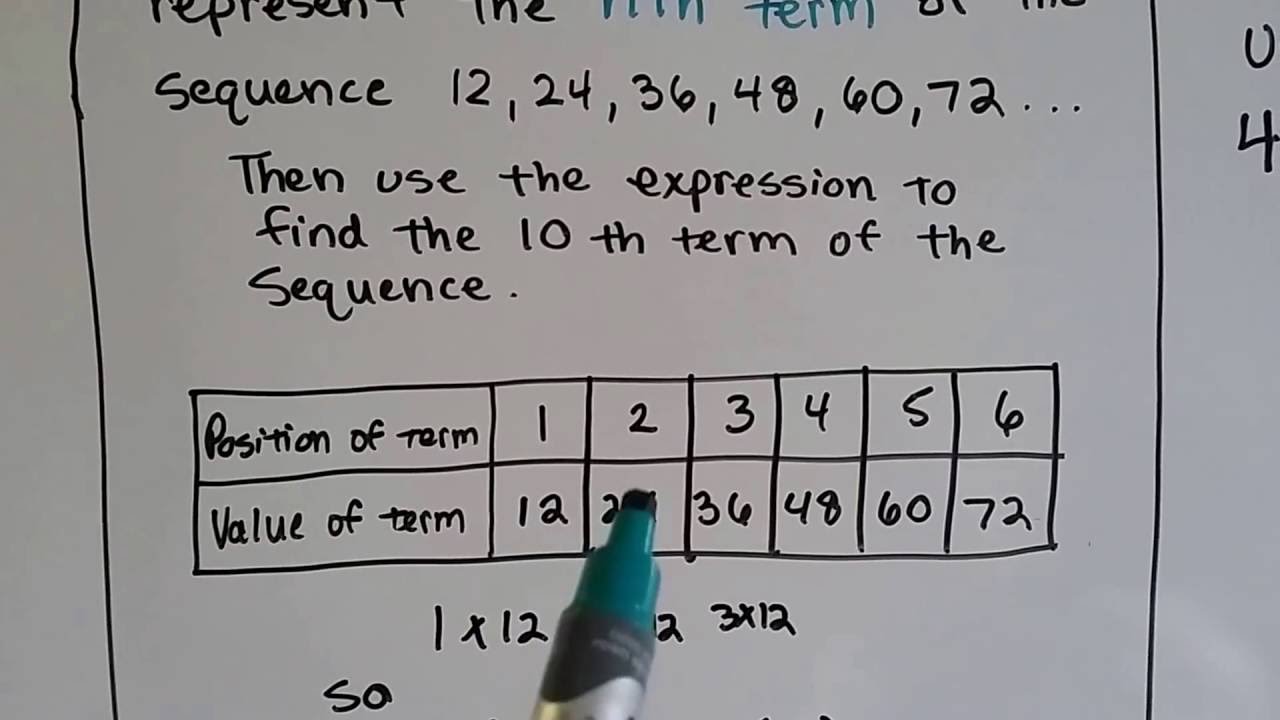
However, notice that this formula is off by 3 for every number in the given sequence. Since each number is six more than the last, the formula will be something like f( n)=6 n. A much easier method is to find a formula f( n) for the nth number in the sequence and then plug in 23 for n. Thus, a straightforward way to calculate the 23rd term is to write out the first 23 terms in the sequence, but this would be very tedious. The pattern is that every number is six more than the last. Thus, the sequence should be -4, -2, 0, 2, 4.ħ. In particular, for every positive number in the sequence is a corresponding negative number. Therefore, in order for the sum to be zero, half of the numbers must be negative. If all of the numbers in a sequence are positive, then the sum of the sequence will also be positive. A sequence of five consecutive even numbers is a sequence of even numbers such that the difference between one number and the next is always 2. Therefore, the first six numbers in the sequence are 2, 6, 18, 54, 162, 486.Ħ. To find the second number, multiply 2 by 3.Ĭontinue this process of multiplying by 3 to find the next four numbers in the sequence. As the problem states, the first number is 2. Therefore, the first six numbers in the Fibonacci sequence are 0, 1, 1, 2, 3, 5.ĥ. Add them to find the third number in the Fibonacci sequence.Ĭontinue this process of adding consecutive terms in the sequence to find the next three numbers in the sequence. As the problem states, the first two numbers are 0 and 1.

The pattern is that every number is half of the previous number. If x represents the first term, subsequent terms are x + 2, x + 4, x + 6, and x + 8. One way to find the correct sequence is to set up and solve an equation. The pattern is that every number is eight more than the last. Find the 31st term in the sequence below.ġ. Determine the next number in the sequence.ġ0. Write the next four numbers in the sequence below.ĩ. Find the 23rd term in the sequence below.Ĩ. Write a sequence of five consecutive even numbers that add to 0.ħ. Write the first six numbers in a sequence in which every number is three times the previous number and the first number is 2.Ħ. Write the first six numbers in the Fibonacci sequence.ĥ. Write a sequence of five consecutive even numbers that add to. After that, each number is the sum of the previous two. Determine the next number in the sequence. The first two numbers in the Fibonacci sequence are 0 and 1. You will receive your score and answers at the. Determine the next number in the sequence.Ĥ. What is a Mathematical Sequence - Quiz & Worksheet Video Quiz Course Try it risk-free for 30 days Instructions: Choose an answer and hit next. Write a sequence of five consecutive even numbers that add to 60.ģ. Determine the next number in the sequence.Ģ.


 0 kommentar(er)
0 kommentar(er)
