
The legs of the Golden triangle are in the golden ratio relative to the base. The angles of a 30-60-90 triangle are in the ratio 1 : 2 : 3. Also when you draw a circumscribed circle in a right-angled triangle then the centre of the circle always lies on the midpoint hypotenuse. An isosceles right triangle is a triangle with 2 congruent sides and angles in which the non-congruent angle measures 90°. A special right triangle with angles 30, 60, and 90 is called a 30-60-90 triangle. Note: To solve this type of question you need to know that the pythagorean theorem only applied for a right angle triangle, and the expression we have already mentioned in the solution part. The circumradius, $$R=\dfrac +1\right) \colon 1$$ This makes it impossible to say that 45 45 90 triangles have the smallest hypotenuses.So to find the ratio we need to know that, Solution: For a right isosceles triangle, the perimeter formula is given by 2x + l where x is the congruent side length and l is the length of the hypotenuse.
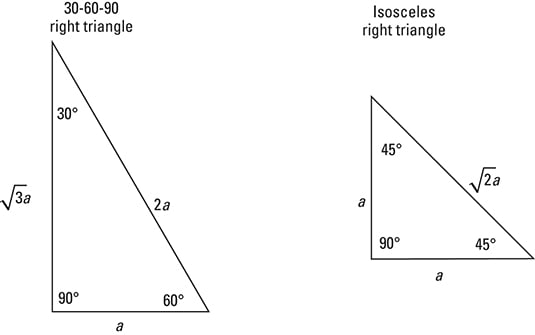
If the non-congruent side measures 52 units then, find the measure of the congruent sides. Since the value of a hypotenuse could be any rational, irrational, or real number, a 45 45 90 triangle could have the smallest hypotenuse of any triangle! However, the infinitesimal nature of these kinds of numbers makes a myriad of possibilities for the length of the hypotenuse of a 45 45 90 triangle. Example 2: The perimeter of an isosceles right triangle is 10 + 52. It is the longest side of any right triangle. The side opposite to the right angle is called hypotenuse. It is a special type of right triangle in which the three interior angles are 45circ, 45circ, and 90circ. Sin 45 \sin 45 sin 45° = 1 2 = \frac 1 : 1 : 2 . A 45circ - 45circ - 90circ triangle is an isosceles right triangle. With the hypotenuse, we have information to determine the following: If you wanted to take a look at more examples of the 45 45 90 triangle, take a look at this interactive online reference for this special right triangle. If a triangle is a right triangle and its isosceles, then the two sides other than the right angle must add up to 90 degrees and they must be equal, so each.

You also happen to know a nice formula to figure out what the length of the hypotenuse is (the Pythagorean Theorem) and we'll show you how it will be used. Since you'll also find that this triangle is a right-angled triangle, we know that the third side that is not equal with the others is the hypotenuse. It is an isosceles triangle, with two equal sides. One of these triangles is the 45 45 90 triangle. For a list of all the different special triangles you will encounter in math. These are the ones you'll most typically use in math problems as well. But for the ones that do, you will have to memorize their angles' values in tests and exams. There's not a lot of angles that give clean and neat trigonometric values. Special triangles take those long numbers that require rounding and come up with exact ratio answers for them. When numbers are rounded, it means that your answer isn't exact, and that's something that mathematicians do not like. Most trig questions you've done up till now have required that you round answers in the end. Special triangles are a way to get exact values for trigonometric equations. Walk through Example and Practice with 45 45 90 triangles.Worksheets are Right triangle trig missing sides and angles, Trigonometric ratios date. Does a rhombus make 45-45-90 triangles? The hypotenuse of an isosceles right triangle is 16 centimeters.
#Isosceles right triangle ratio how to


 0 kommentar(er)
0 kommentar(er)
